La varianza es la representación de una medida en la que unos valores tomados pueden variar unos de otros en la muestra o en la población.
Al calcular la varianza puedes estudiar el comportamiento estadístico de dicha población, reconociendo el valor y las probabilidades en dichos dígitos o grupo de muestra.
Dentro del cálculo de la varianza se debe cumplir una regla, y es que los datos tomados aleatoriamente de la muestra o de toda la población debe mantener valores típicos o relacionados, es decir, valores cercanos a la media y entre ellos, ya que, si se presentan valores atípicos o con variables muy grandes y en minoría, los mismos no son representativos de la población y por tanto no deben tomarse en cuenta.
Calcular la varianza muestral
La varianza de una muestra o una varianza muestral corresponde al valor calculado de la suma total de todos los datos de la muestra (Xᵢ) con la resta del valor de la media (x̅ ) entre el número de valores obtenidos menos uno (n-1)
Se toma el valor menos uno para apreciar el valor de la muestra con relación a la población.
Suponiendo que se obtiene en la tabla de valores:
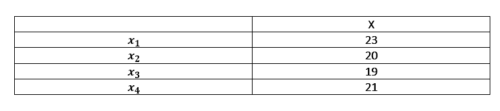
Se aplica la siguiente fórmula de la varianza muestral:
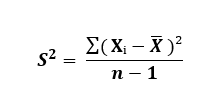
Para obtener el valor de la media ( x̅) se suman todos los valores de X y se divide entre el número de valores tomados.
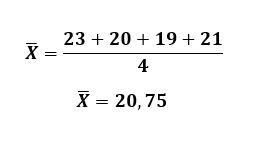
Una vez calculada la media x̅, se procede a sustituir los valores de las sumas

La desviación estándar de una muestra
A diferencia de la desviación estándar de una muestra, la unidad de la varianza se expresa en el valor elevado al cuadrado.
Para determinar la desviación típica o estándar de una muestra, únicamente requieres establecerle la raíz cuadrada para eliminar dicho exponente.
En este caso, quedará representada la desviación estándar como (s) y el valor sin elevar al cuadrado.
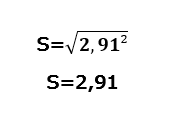
Calcular la varianza de una población
La varianza poblacional representa el estudio de una población completa, es decir, que tomarás todos los valores para determinar la varianza.
Asumiendo que los valores de la tabla anterior corresponden a una población entera, el ejemplo se basará en la misma tabla de valores.

La fórmula se basa en el mismo principio de la sumatoria de todos los valores de cada elemento de la población (Xᵢ) menos el valor de la media (µ) elevados al cuadrado.
Finalmente corresponderá dividir el resultado entre el número de datos tomados de la población (n).
Para esto, se implementa la fórmula para calcular la varianza de una población σ²:
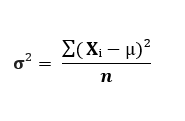
Para calcular el valor de (µ) se procede a calcular el valor de la media de todos los datos tomados. En este caso, se suman todos los valores de X y se dividen entre n, que es el número de datos tomados.
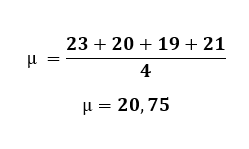
Al obtener el valor de la media, necesitarás sustituir los valores de la fórmula en las restas y sumas consecutivamente.

